Gamma与对冲损益之
数据实证研究
1. 研究思路
在上一份报告中,我们从理论上分析了Gamma和对冲损益之间关系的积分表达式,这次我们利用实际数据去检验对冲损益的变化。
我们利用一个月的股指期权的仿真数据和当月股指期货的,然后固定不同水平的对冲波动率去进行gamma交易,然后检验最后的盈亏情况。
2. 研究假设
第一步的实证研究我们并不考虑交易费用的存在;
设定对冲频率每天收盘价对冲;
所有价格以收盘价计;
设定对冲数量可以精确到7位小数,即可以购买0.0001份指数;
这里分别用股指期货和股票指数来为期权做定价模型,以已实现波动作为对冲波动率条件下,以pl绝对值最小为标准,筛选最优期权对冲定价模型。
3. 数据样本
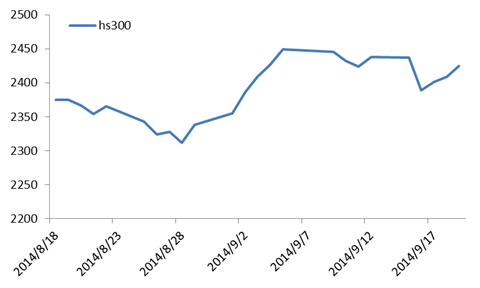
图 1 hs300指数价格真实走势
其中,该价格路径波动率年化为12.7%
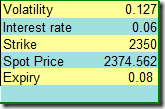
4. 初始状态
在t0时间点,沪深300指数收盘价为2374.6;
行权价为2350的认购期权此时价格为74.4;
BS定价模型下的隐含波动率为20.02%。
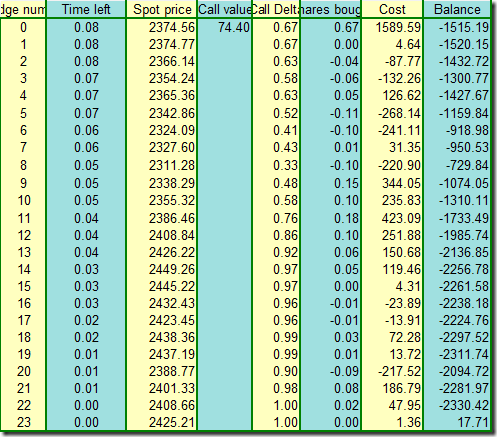
5. 对冲过程
这里的设想是卖出期权,同时进行delta,不考虑保证金等其他费用,并且连续对冲。
卖出期权的权利金收入为74.4,对冲标的买入费用1589.59,则期初资金投入1515.19.
数据选取的是2014/8/18至2014/9/19这一段时间的沪深300指数数据。
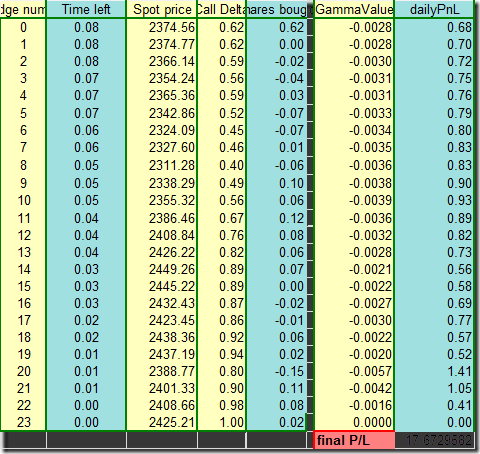
5.1. 使用realizedVol进行对冲回溯
最后的对冲盈亏为17.71。
对冲示例如下:
基本参数是:
对冲结果
对冲过程如下:
整个过程解释如下:
我们用12.7%波动率对期权进行对冲,最后对冲盈亏为17.17。
那么实际上所卖出的期权,对我们来说,成本为74.40-17.17exp(-rT)=57.31。接近BS73下,期权在realizedVol的理论价格。
5.2. 使用impyVol进行对冲回溯
在购买期权的时候,我们并不知道期权存续期间的已实现波动率是多少,特别在hmm系统里面,我们实际上主要参考的是市场隐含波动率参数来计算delta进行对冲。
如果我们波动率参数设置为20.2%,也即对应了期权的卖出价,那么最后的对冲结果是
也就是说,我们如果以74.4卖出这个期权,并在收盘前用隐含波动率对冲,最后的盈利为21.47%(相对于期权价值)。
从上面两个结果可以看出,虽然利用较低的已实现波动率,最后的收益率更高一点,但是二者相差并没有想象中的那么大。
风控部门往往要求交易员用隐含波动率进行deltahedge,从我们上面的实验结果可以看到,即使隐含波动率和现实波动率相差较大的时候,实际上对盈亏的影响并没有那么大。
6. 对冲频率VS对冲波动率
从上述实证我们发现,相比之下,对冲频率对PnL有着更为明显的影响
这里我们提供了一组相同价格路径下,不同对冲波动率设定的对冲损益。这里对冲频率和上文保持一致,都是对冲23次。其他设定也保持一致,期权的卖出价为74.4,而期权的已实现波动率对应的理论价为55.62,二者差距为18.78。
实际上下表中的所有值都在这个值附近(如果波动率取值极大,会偏离这个值)。
表 1 不同波动率下对冲损益
而相比对冲波动率,对冲频率的不同会对对冲误差造成更为明显的影响,我们还是利用上述价格路径进行研究,但是对价格路径进行等间隔抽样,也就是原来每天对冲一次,这里设置为每隔一天对冲一次,每隔两天对冲一次,每隔3天对冲一次,每隔4天对冲一次,每隔六天对冲一次,每隔8天对冲一次,每隔12天对冲一次,以及就对冲一次。这里的对冲波动率都设定为完整路径的已实现波动率,也即12.7%(需要注意的是,抽样出来的路径的波动率,和完整路径的已实现波动率并不完全一致)。
从下面的统计中可以发现,不同对冲频率下,最后的损益非常不稳定,这是因为实际上由于对冲次数较少,但对冲次数过少时,波动率这个参数需要时间去体现,当对冲此时过少时,波动率参数本身已经失去了存在的意义,到期时的价格更多的体现出的是概率上的随机变量,失去了统计上的意义,因此最后的对冲损益也是一个随机数,并不能得到对冲频率越少,对冲损益越大,这样的结论。
能下的结论是对冲频率越高,对冲损益越趋于稳定,但是这个结论本身在我们这里无法体现,还需要进一步的实证 (这一结论对delta对冲有效,对于止损策略无效)[1]。
|
HedgeNum |
24 |
12 |
8 |
6 |
4 |
2 |
1 |
|
final P/L |
17.71 |
61 |
55.62 |
58.64 |
45.58 |
28.44 |
25.5 |
7. Gamma与对冲损益
上文的研究我们还只是在进行delta Hedge,也可以看到,即便用已实现波动率做对冲,仍然会有对冲误差。这个原因我们在前面的理论分析中有过论述:
7.1. realizedVol下的对冲损益
从上面公式上看,如果对冲波动率和已实现波动率一致,那么PnL应该为0,但是实际上波动率参数本身也是一个随机过程,事实上,不同的时间窗口,对应的波动率都是不同的,而这一特性我们本身很难描述。
由于我们假定交易都是以收盘价进行,因此,最合适去描述这段时间的已实现波动率指标就是close2close的已实现波动率。
而上述realizedVol下对冲的pnl为17.71,最主要的原因是期初我们期权卖出价是74.40,而不是realizedVol下的理论价55.62,这二者之差为18.78。也就是说,如果我们当初的卖出价是18.78,那么这样的对冲过程中,我们PnL为-1。这和期权卖出价相比,为2%左右,并不是一个很大的误差。
如果我们用realizedVol用作对冲波动率,那么我们的gamma损益为0,而本身17.71的总体对冲损益,就应该归结到其他损益上面。我们认为这里应该这样认识这个问题:如果我们用realizedVol对冲,那么我们实际上在期初时刻,就认定期权波动率为0.127,而我们卖出的波动率是0.20,因此这17.71绝大部分是vega收益。
数据也提供这种认识,期初vol为0.2下的vega值为261,波动率降低带来的收益为19.1,vol为0.127下的vega值为248,对应的vega收益为0.181。二者和对冲损益17.71相比,差别不是很大。
因此我们可以这样理解,如果对冲波动率和隐含波动率不同,那么我们在对收益进行分析的时候,第一步可以计算出卖出瞬间的波动率收益(![]() ),剩下来才是对冲过程中实现的Gamma收益。
),剩下来才是对冲过程中实现的Gamma收益。
7.2. implyVol下的对冲损益
事实上我们在建仓时,并不知道期权存续期间的已实现波动率是多少。虽然有很多方法可以计算历史波动率,但实际上,用这些波动率来预测未来的波动率,很难说是一个可靠的指标。
市场隐含波动率,一定程度上反应了市场参与者对未来波动率的预期,很多做市软件和系统都是基于市场隐含波动率的模型来计算delta的(并不是用实时的市场隐含波动率,而是基于市场隐含波动率,拟合波动率模型,确定theoVol,然后用这个相对稳定的theoVol计算delta)。
上面提到,close2close的已实现波动率是我们所能度量的标的资产波动率的最佳近似,因此我们认为这段时间标的资产的真实波动率就是realizedVol。
那么我们用上述的PnL公式,计算对冲的PnL:
从上面统计结果可以看出,我们用(*)式计算的PnL和我们上面实证统计的利用已实现波动率进行对冲的Pnl非常接近,但是和用implyVol计算得到的PnL差距稍大。
对于上述公式,我们理解,上述公式计算的是隐含波动率在BS模型下的期权成本,和期权的对冲成本的差距。也就是说,我们卖出一个74.4的期权,同时按照卖出的隐含波动率进行delta对冲,我们最后的Gamma收益为17.67。
也就是说,不管期初隐含波动率是多少,我们只要按照隐含波动率做对冲,最后对冲的收益总是接近于期权的真实价格,而不是对冲波动率对应的期权的价格。
换句话说,对冲出来的期权的成本更多的取决于期权的真实波动率,而不是我们对冲所用的波动率。
这个值和我们上面利用隐含波动率进行对冲的PnL值15.97并不完全一致,但是误差在5%以内,这可以解释为真实波动率并不是固定的已实现波动率(但我们无法对这一猜想进行实证)。
在上面的数据实证中,我们发现如果对冲波动率设置为隐含波动率,那么最后的对冲损益,基本上和gamma损益非常相近。下面我们用更多的波动数据取检验这个结论,都支持结论:如果用隐含波动率对冲,那么最终对冲损益是gamma实现的损益。
表 3 不同隐含波动率下的对冲损益
8. 模拟路径下的对冲过程
上述波动率路径是真实的指数价格波动路径,但是从价格变化的图形中,我们也能看出,波动率值较低,并且看不出明显的变化。
如果真实波动率没有明显变化,用已实现波动率计算的期权价格,和最后的对冲成本(已实现波动率下的),从理论上来说,应该是非常接近的,实际上我们最后实验的结果误差在2%左右,也基本在可以接受的范围内。
上面所有的研究,不管是对冲波动率,还是真实波动率,我们都设定为一个固定值,因此Gamma损益和最后的对冲损益大小基本相同。
但是如果波动率出现明显的变化,那么情况会是怎么样,我们继续研究这个问题。
8.1. 波动率断点模型
模拟价格路径分为两段,前一半标的真实波动率为50%,后一半标的真实波动率为10%。
不同样本数量对于波动率方差的计算影响显著,在大样本下,模拟的价格路径的方差才接近。因此我们这里将路径拉长,也即对冲的次数增加,直到价格路径的已实现波动率接近我们路径生成的参数。
在路径生成完成后,我们在对路径的已实现波动率进行衡量,前一半的已实现波动率为55.10%,后一半的已实现波动率为10.4%,已经较为接近路径生成的参数。
对于路径整体的已实现波动率进行衡量,其路径整体波动率为39.6%。
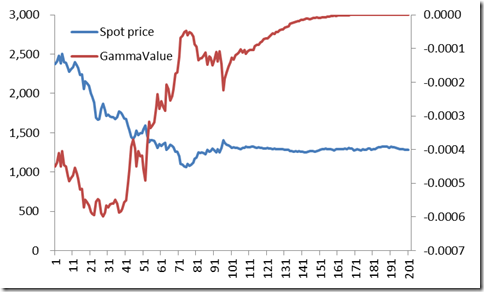
图 2 价格路径和波动率路径
当期权卖出波动率为已实现的全路径隐含波动率39.6%时,此时我们对冲损益为-42.58(-10.9%),而对应的gamma损益为-31.7,二者产生了较为明显的差距。
对于这个结果,我们可以这样理解,在期初阶段gamma绝对值较大,此时真实波动率大于对冲波动率,因此这一段是不断发生对冲损失。在期末阶段,gamma绝对值值较小,而真实波动率小于对冲波动率,虽然有对冲收益,但是难以抵减期初的对冲损失,因此期间对冲收益为负。
实际上,当我们的对冲波动率和路径波动率参数保持一致时(即用路径的已实现波动率进行deltahedge),那么我们可以最终的对冲误差在1%左右。也就是说,在对冲时,路径波动率和隐含波动率不一致的部分,会立刻产生vega损益,但是这个由于我们并不卖出期权,这种vega损益并不会立即在账面上实现。
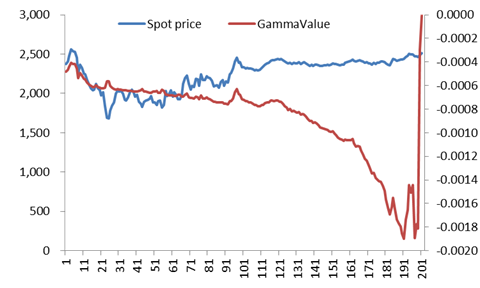
对于另外一组路径,全路径已实现波动率为37%,前一半标的已实现波动率为51.6%,后一半标的已实现波动率为9.3%。当期权卖出波动率为已实现的全路径隐含波动率37%时,此时我们对冲损益为91.41(24.5%),而对应的gamma损益为85,虽然路径波动率属性和上一情景类似,但是最终对冲盈亏迥异。
图 3 价格路径和波动率路径
综上,对于对冲者来说,最合理的对冲波动率就是标的的真实波动率,这样可以最小化对冲误差。真实波动率和期权卖出价对应的隐含波动率之差的vega收益实际上也可以立即在理论上实现。
固定用某一个波动率进行对冲,其最终对冲盈亏大小和期权Gamma路径(实际上也就是期权价格路径)有关。
[1] John Hull 期权、期货以及其他衍生品(第六版中文版),p219